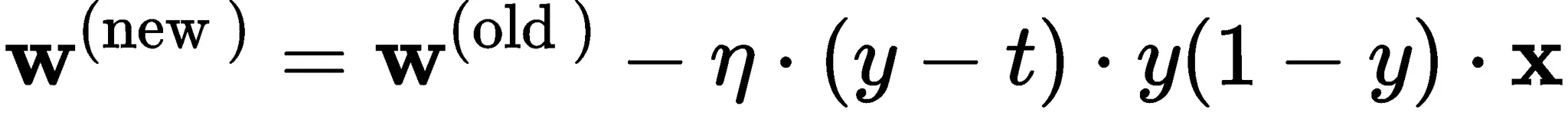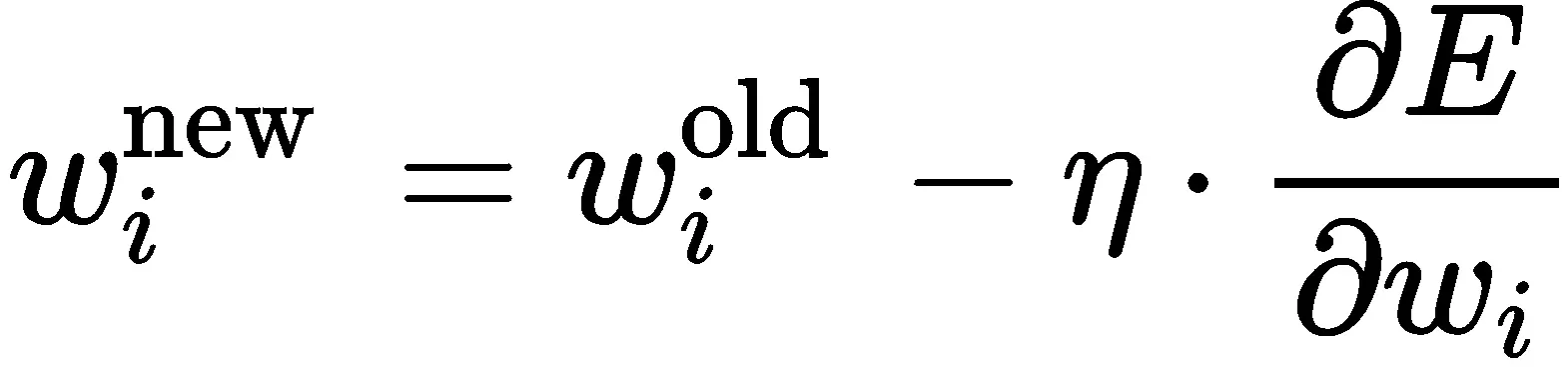신경망 학습에서 가중치를 업데이트하기 위해 오차 함수(E)의 그래디언트를 계산하는 과정은 매우 중요합니다. 여기서 우리는 시그모이드 활성화 함수를 사용하는 신경망에서 오차 함수의 그래디언트를 어떻게 계산하는지 살펴보겠습니다.
(1) 오차 함수 \(E\)
주어진 오차 함수는
\[E=\frac{1}{2}(t-y)^2\]
입니다. 이는 실제 값 \(t\)와 예측 값 \(y\) 사이의 차이를 나타내는 평균 제곱 오차 함수입니다. 이 함수를 최소화함으로써, 우리는 모델의 예측을 실제 값에 더 가깝게 만들 수 있습니다.
(2) 시그모이드 함수와 그 미분
시그모이드 함수 \(\sigma(u)\)는 다음과 같습니다.
\[y=f(u)=\sigma(u)\]
그리고 시그모이드 함수의 미분은 다음과 같은 성질을 가집니다.
\[\frac{d \sigma(u)}{d u}=\sigma(u) \cdot (1-\sigma(u))\]
(3) 입력에 대한 선형 조합
입력 \(x_i\)와 가중치 \(w_i\)의 선형 조합으로 구성된 \(u\)는 다음과 같습니다.
\[u=\sum_{i=0}^K w_i x_i\]
그래디언트 찾기
가중치 \(w_i\)에 대한 \(E\)의 그래디언트를 구하기 위해 연쇄 법칙(chain rule)을 사용합니다. 먼저, 오차 함수 \(E\)를 가중치 \(w_i\)에 대해 편미분합니다.
오차 함수의 미분
\[ \frac{\partial E}{\partial w_i} = \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial u} \cdot \frac{\partial u}{\partial w_i} \]
각 항을 구체적으로 계산해 보면:
1.
\(\frac{\partial E}{\partial y}\): 오차 함수 \(E\)를 예측 값 \(y\)에 대해 미분하면,
\[ \frac{\partial E}{\partial y} = (y-t) \]
2.
\(\frac{\partial y}{\partial u}\): \(y=\sigma(u)\)이므로,
\[ \frac{\partial y}{\partial u} = \sigma(u) \cdot (1-\sigma(u)) = y \cdot (1-y) \]
3.
\(\frac{\partial u}{\partial w_i}\): \(u\)를 가중치 \(w_i\)에 대해 미분하면,
\[ \frac{\partial u}{\partial w_i} = x_i \]
그래디언트 표현
따라서 가중치 \(w_i\)에 대한 \(E\)의 그래디언트는 다음과 같습니다.
\[ \frac{\partial E}{\partial w_i} = (y-t) \cdot y \cdot (1-y) \cdot x_i \]
이를 통해 가중치 업데이트 식을 다음과 같이 쓸 수 있습니다.
\[ w_i^{\text {new }} = w_i^{\text {old }} - \eta \cdot \frac{\partial E}{\partial w_i} \]
\[ \mathbf{w}^{(\text {new })} = \mathbf{w}^{(\text {old })} - \eta \cdot (y-t) \cdot y \cdot (1-y) \cdot \mathbf{x} \]
여기서, \(\eta\)는 학습률을 나타내며, 이 과정을 통해 신경망은 오차를 최소화하는 방향으로 가중치를 조정하게 됩니다. 이러한 방식으로 그래디언트를 계산하고 가
중치를 업데이트하는 과정은 신경망이 학습하는 기본 메커니즘입니다.